This is part three of the 12 days of Covidmas. Visit Covid Corner to read parts one and two!
Building on last time, the evidence is quite clear that when we look at long-term mortality data, Covid will barely register. That said, it is obviously a disease that is very contagious, and does have the ability to kill people.
Humans are very bad at understanding risk, assessing risk, and acting rationally based on risk. We have a hard time conceptualizing things that might happen. People deal best with certainties, and “if I do this then that will happen” scenarios. We all know this intuitively, but it has also been well documented in psychological research.
As a result, we tend to be very risk averse, as we imagine the worst case scenario and then treat it as though it will happen. I’ve seen people do this with Covid, as I’m sure you have also. If we meet up, then one of us will have Covid, then I’ll get it, and then I’ll die or give it to someone I know and they’ll die! We better not risk it.
In behavioral therapy terms, this is called catastrophizing, and it’s a psychological distortion. It’s not healthy and therapists have been helping people who do this for decades via cognitive behavioral therapy (CBT).
So with that said, I want to go down the road of explaining the risk due to Covid based on facts and science for a fairly typical scenario: a multi-generational, multi-household Thanksgiving dinner.
This is instructive as the exact same process could be applied to Christmas activities. But it is also instructive as it provides an analytic framework for comparing the risk of different actions based on known scientific research. While doing this all the time would be paralyzing, it makes sense to do it in the case of a novel virus: we can put the risk posed by Covid in terms of activities we have much more experience facing over the years.
So let’s dive in!
This is going to get a bit, uh, statistic-y. So many in my network will be able to follow it, but many may not. I’ll do my best to explain this in a way that is broadly understandable.
If we focus purely on the risk of death, a person’s risk due to Covid is as follows:
P(someone at the gathering has Covid) x P(Covid is transmitted to this person) x P(Covid causes this person’s death)
Now, this does get more complicated as you have more people at a gathering. But there is also relevant data to assess each of these points. As such, let’s take each of these three probabilities separately, and then we’ll tie it all together.
Probability someone at the gathering has Covid
A basic way to approximate this would be to take the number of people currently infected in a person’s geography and divide that by the population to get an estimate for the chance that someone has Covid. So if someone came from New York where there are 315,000 active cases and a population of about 20,000,000 then we could say that a New Yorker has a 1.6% chance of being infected.
But we can make this more robust in two ways. One, we can account for the fact that a substantial amount of Covid cases are going about undetected because they have few if any symptoms. And two, we can assess this at a smaller geographic level, so use county instead of state.
Fortunately, there exists a site for this! Covid19 Projections is a project done by an MIT graduate who has built models that estimate overall spread at a county-by-county level. Based on this, I can tell you that my home county, Dallas County, has about 2.4% of the population currently infected. So barring other data about my lifestyle, this would be a reasonable assessment of the chance that I have Covid.
These numbers are all going to be fairly low (the average nationally is 2.5% as I write this). But obviously as you get more people in a room, the chances that one of them having Covid goes up. At this 2.5% national baseline, if you have 10 people in a room, there is a 23% chance that at least one of them has Covid. If you take that up to 50 people, there’s a 72% chance that at least one of them has it.*
Probability Covid is Transmitted
Next, we get to the point of saying: if someone brings Covid to our dinner, what is the odds for that to be transmitted to everyone else?
This too could be tricky, and would obviously depend on what type of gathering it was and what precautions (if any) you put in place. But we can get a baseline and adjust from there.
For my baseline, I used the CDC study of a 55 person wedding that was covered in the Los Angeles Times a few months ago. In this case, at least one person had Covid going in, and when all was said and done, 30 of the 55 attendees ended up with the ‘roni. This gives us a 54% baseline probability.
Now this number probably includes some secondary infections, as a wedding group includes many families that go back and live with each other. So not all of the 30 people who got the ‘roni got it at the same time. Still though, this approximates a Thanksgiving (or Christmas) get together, and so the 54% number I felt was accurate in assessing our risk.
Lastly, let’s say you do plan to take some interventions, which this wedding largely did not. We could suggest that masks will reduce the odds of transmission by a modest amount, say 10%. That’d reduce the odds of transmission down to 37% and thus make the entire gathering safer. You could apply the same logic with doing an outdoor gathering, et cetera.
Now on to our last risk:
Probability that someone infected with Covid dies from it
Last but certainly not least, we get to the most important one: the odds that if someone gets Covid that they will die from it.
This is also the risk where it is most critical to customize it based on the attendees. It’d be fairly simple to stick with a 2.5% per person risk of bringing Covid in and a 41% chance of transmission. But the rate of death varies substantially based on the characteristics of the people attending.
And it is just this point that has been wildly underreported and inaccurately reported. A conspiracy theorist would say that this is part of a larger plot. Hanlon’s razor would suggest that this is just because journalists are not smart humans.
Regardless, there are fortunately studies that look at both age and the presence of high-risk pre-existing conditions in approximating death rate due to Covid. It has been broadly communicated and is widely accepted that these are the two largest risk factors. But what has not been communicated is what that actually means for risk at a personal level when you combine the two factors.
The study I’ll reference, which comes from Stockholm University and was published in the British Medical Journal does align with the data we have from the CDC when you triangulate out from what has been shared. Here is the table of the probability of death due to Covid:
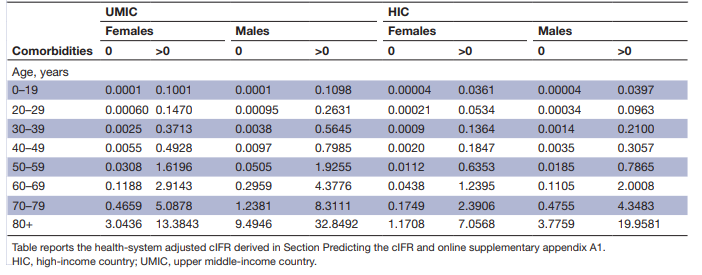
Taking myself as an example: as a 30-something year-old male with no pre-existing conditions, my chance of death due to Covid is 0.0014%.
Now if you were to take my grandfather – an 80-something male with pre-existing conditions, his chance of death would be 19.95%. That is a HUGE difference. He’s quite literally 14,000 times more likely to die from a Covid infection than I am.
Now it is worth taking a jump here to cover one point: humans are really bad at understanding very large and very small numbers. We can all see 19% above and say “oof, that’s pretty bad – a 19% chance of death? No thanks!” We know that’s roughly 1 in 5 times and we can all conceptualize that easily.
But this is harder when I give you a number like 0.0014%. We know that’s small, but our thinking may go, “Well, it’s bigger than zero. I mean, there’s a chance of death! That’s bad. I better not do this.”
The challenge is that everything we do has risk. In fact, just by virtue of being a 30 to 39 year-old male in the U.S., there’s roughly a 0.20% chance that I’ll die in the next year anyway (source). Put another way, 0.2% of all 30-something year-old men die every year. Cancer, car accidents, violence, drug overdoses or suicide – the sad fact is that the world is a dangerous place and life is fragile. Do you want a good kick in the rear that life is short? Look at an actuarial table.
But this also helps us conceptualize that 0.0014% chance. Say I knew for sure that I would get Covid in the coming year. My risk of death would go up from 0.2% to 0.2014%. In case you can’t tell – those two numbers are practically the same. As someone relatively young and relatively healthy, I should be much more concerned about many other potential risks over the coming year.
Here are a couple other ways to conceptualize that 0.0014% chance of death:
My chance of death if I get Covid is about 1 in 71,000. I would survive the other 70,999 times.
The chance of death in a car accident in a given year is 0.01% or 1 in 10,000. So getting the ‘roni (for me) is equivalent to the risk I face from about two months of my normal car driving activity.
Farmers have the 7th most dangerous job in America – they have 24.7 deaths per 100,000 people each year. This risk is 17 times greater than my risk of death from the ‘roni. Or equivalent to me working as a farmer for 21 days.
The odds of death from going bungee jumping is 0.0002%. So the chances that I die from the ‘roni if I catch it are the same as doing seven bungee jumps.
I would strongly suggest that you look at your “personalized” chance of death on this chart (and obviously those who you would plan to meet with). A general hueristic is that anyone who is under 60 years old and has no known conditions is incredibly safe. Even the worst death rate in that bucket puts the risk of death at 0.02% – or the equivalent of driving a car for two years.
Bringing It All Together
Lastly, we can bring all these factors together and not just estimate the risk of an individual surviving a Thanksgiving dinner, but estimate the odds that anyone attending would die.
I’ll spare you the details at this point. Butlargely, this just involves multiplying the risks together. If there is a 10% chance that someone has the ‘roni, a 41% chance they transmit it, and then I have a chance of death of 0.0014%, then Thanksgiving dinner would pose a 10% x 41% x 0.0014% risk to me. This takes my chance of death from being microscopic to being almost subatomic, if we’re speaking colloquially.
As noted, I ran this model for all of our eight attendees at Thanksgiving. The end result? We had a 99.95% chance of all of us surviving, or 1,999 out of 2,000 times.
Here again we suffer from poor conceptualization of small numbers. Here’s what that looks like visually:

As you can probably expect, we deemed this safe enough to gather, although my grandparents chose not to attend. And, not surprisingly, we all survived the gathering (and had a great time)!
If there is one thing you should take from this, it’s that the ‘roni presents drastically different risks depending on the person, and that your risk is, likely, a lot lower than you’ve probably been led to believe.
If you are like me (under 60 and healthy), then the risk posed to you is so low that if you were looking to be consistent, you would stop driving anywhere and certainly lock yourself inside each winter due to the increased chance of death from the flu and pneumonia.
Obviously a few things could change this calculation. If you live with or are in regular contact with at-risk relatives, you may choose to be more cautious. If you are worried hospitals could overflow, that could justify a more cautious approach. And if you are worried about the potential for long-term complications from Covid, you could be more cautious.
On these latter two points (hospitalization rates and long-term complications from Covid), we’ll cover them each in their own piece on subsequent days. Suffice to say, I don’t view either as having a significant impact on the calculations above, but we’ll get into why that’s the case.
It worth one last reflection on the first thing I mentioned – those at high risk or those who live with someone who is at a high risk of death from the ‘roni. I feel bad for anyone in this bucket. It presents a real threat and a real reason to fear interaction with other people.
But the reality is that no matter what the rest of us do, these people would need to take the same preventative actions anyway. Even if all of us who could lockdown did so, the virus would still be circulating among the 40% of American workers (55 million workers) whose jobs are essential. And their families would be susceptible as well. We’ll get into this more as we discuss the travesty of lockdown policies, but I did want to lay down that marker as we wrap up today’s post.
Lastly, my aptly named “Thanksgiving Death Model” is, of course, an adjustable Excel sheet that anyone could use to assess their own risk of Christmas gatherings and make personalized decisions rather than following irrelevant broad brush suggestions from the government. If you’d be interested in using this, let me know and I will clean it up and provide as a resource.
*This calculation isn’t as straight forward as 10*2.5% = 25%. Basically because there is some chance that multiple people bring in the ‘roni, the chance that anyone has it is actually slightly lower. The calculation is 1- (1-0.023)^10 = ~23%



